ORIGENES DE LOS NÚMEROS.
Los orígenes de los números son muy antiguos, muchas culturas antiguas los utilizaron de manera práctica, de esta manera, podemos encontrar a lo largo de la historia humana, diversas culturas o tradiciones en los cinco continentes conocidos que, a pesar de no tener ningún contacto entre ellas, identificaron la importancia de numerar y contar en el devenir humano y, por ello, desarrollaron sus propias técnicas numéricas, con las que podían decodificar e interpretar los acontecimientos sucedidos y prever el futuro cercano (esta última práctica, se circunscribió, en un principio, a los ciclos agrícolas de siembra y recolección y a los ciclos atmosféricos, celestes y estacionales).
1. Los números en la cultura sumeria y babilónica (4000 a.C.)
La cultura sumeria emergió en el sur de Mesopotamia (“tierra entre dos ríos”) en las áreas comprendidas entre los ríos Tigris y Éufrates del actual Irak, y llegaba hasta el noreste de la actual Siria.
El sumerio es la primera lengua escrita conocida, su escritura se llama cuneiforme porque sus trazos tienen forma de cuña; se puede apreciar este tipo de trazado en sus números:

De esta compleja y enigmática cultura, hemos heredado, entre otras cosas, la notación posicional de los números, es decir, un número para las unidades (en el extremo derecho de la cifra), otro número para las decenas (a continuación y a la izquierda de las unidades), otro número para las centenas (a continuación y a la izquierda de las decenas), etcétera.
El sistema numérico sumerio era de base sexagesimal, esta base la utilizamos en la actualidad para medir el tiempo (horas, minutos y segundos), para determinar la posición geográfica (longitud y latitud) y para medir los ángulos geométricos (grados).
2. Los números en la cultura fenicia (1200 a.C. - 539 a.C.)
La cultura fenicia floreció en las áreas costeras de Israel, Siria y Líbano (región conocida antiguamente como Canaán).
La numeración fenicia la constituían 6 símbolos (o glifos) básicos que, combinándose entre ellos, podían representar cualquier otra cantidad.
Los 6 símbolos básicos que utilizaron los fenicios (y posteriormente los cartagineses) se indican a continuación:
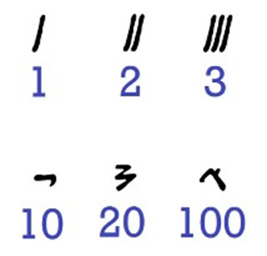
3. Los números en la cultura egipcia (3000 a.C.)
El sistema de numeración egipcio es tan antiguo como la propia escritura jeroglífica egipcia; con dicho sistema podían representar cantidades millonarias; su base era decimal.
Los números en la cultura egipcia, se podían escribir de dos maneras, utilizando la escritura jeroglífica o bien la escritura hierática (la cual permitía a los escribas escribir de forma rápida).

4. Los números en la cultura maya (2000 a.C. – 1546 d.C.)
La civilización maya habitó en los territorios de Honduras, El Salvador, Belice, Guatemala y el sur de Méjico.
La numeración utilizada por los antiguos mayas, era de base vigesimal, es decir, las cantidades se agrupaban en veintenas (de 20 en 20).
Los mayas disponían de tres maneras de representar los números:
- Mediante puntos y rayas.
- Mediante puntos y rayas.
- Con glifos antropomorfos (cuerpo completo).
Los mayas utilizaban los números para medir el tiempo, no realizaban con ellos operaciones matemáticas. Conocían y utilizaban el número cero (0), el cual era tratado como un número más.
La numeración mediante puntos y rayas era la que se indica a continuación:
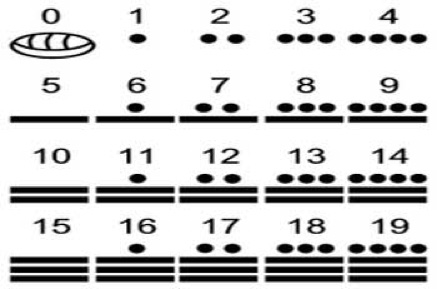
5. Los números en la cultura de la antigua Grecia (1200 a.C. – 146 a.C.).
El sistema de numeración en la antigua Grecia utilizaba las letras del alfabeto griego. Se pueden distinguir dos sistemas diferentes, el ático y el jónico (posterior).
5.1. Sistema ático o acrofónico.
El sistema de numeración más antiguo fue el ático (o acrofónico) cuyo funcionamiento era similar al sistema de numeración romano. Se basaba de acuerdo con la siguiente simbología:
Ι = 1, Π = 5, Δ = 10, Η = 100, Χ = 1000 y Μ = 10 000.
Este sistema se denomina “acrofónico” porque (exceptuando el símbolo para el “1”, un único trazo vertical) los símbolos (o glifos) procedían de la primera letra de cada número en escritura arcaica:
- πεντε (pénte, “cinco”)
- δεκα (déka, “diez”)
- ηεκατον (hekatón, “cien”)
- χιλιοι (chílioi, “mil”)
- μυριας (myrías “diez mil”)
El símbolo o dígito Π (πεντε, pénte, 5) se podía combinar para formar los números 50, 500, 5000 y 50 000, añadiendo, a dicho dígito, versiones diminutas de los símbolos para obtener multiplicaciones de diez en diez:
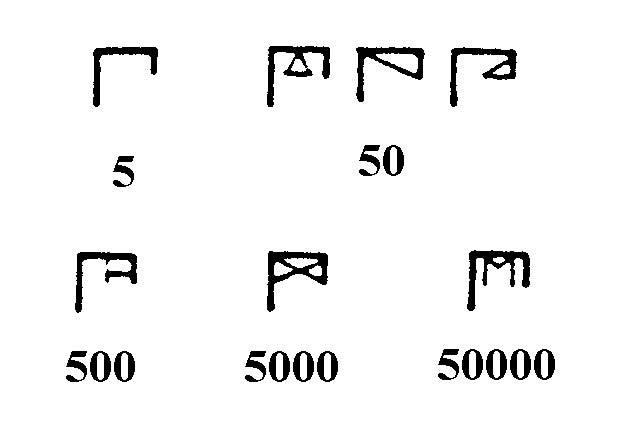
5.2. Sistema jónico (a partir del siglo IV a.C.).
A partir del siglo IV a.C., el sistema acrofónico se fue sustituyendo por un sistema alfabético decimal, llamado jónico. A cada cifra de unidad (1 - 9) se le asignó una letra, a cada decena (10 - 90) otra letra y a cada centena (100 - 900) otra letra. Este sistema requería 27 letras, por lo que se añadieron otras tres antiguas letras:
- Digamma (Ϝ) o stigma (ϛ) para el 6.
- Qoppa (ϙ) para el 90.
- Sampi (Ϡ) para el 900.
|
Letra |
Valor |
Letra |
Valor |
Letra |
Valor |
|
α´ |
1 |
ι´ |
10 |
ρ´ |
100 |
|
β´ |
2 |
κ´ |
20 |
σ´ |
200 |
|
γ´ |
3 |
λ´ |
30 |
τ´ |
300 |
|
δ´ |
μ´ |
40 |
υ´ |
400 |
|
|
ε´ |
5 |
ν´ |
50 |
φ´ |
500 |
|
ϝ´ / ς΄ / στ´ |
6 |
ξ´ |
60 |
χ´ |
600 |
|
ζ´ |
7 |
ο´ |
70 |
ψ´ |
700 |
|
η´ |
8 |
π´ |
80 |
ω´ |
800 |
|
θ´ |
9 |
ϙ´ / ϟ´ |
90 |
ϡ´ |
900 |
Para poder distinguir los números de las letras, se colocaba un acento al final del grupo numérico; este sistema se basaba en el principio de la suma, así, los valores numéricos de las letras se sumaban para formar el total. Por ejemplo, el 352 se representaba como τνβ´ (300 + 50 + 2).
Para representar números del 1 000 al 999 999 se vuelven a usar las mismas letras de las unidades, decenas y centenas, añadiendo un acento agudo invertido o una coma para distinguirlos. A modo de ejemplo, el 5007 se representaba como ͵εζ´ (5000 + 7).
Los antiguos griegos no utilizaban ningún símbolo para representar el cero.
6. Los números en la cultura de la antigua Roma (1200 a.C. – 146 a.C.).
El sistema de numeración romano se desarrolló en la Antigua Roma y se utilizó en todo el Imperio romano.
Es un sistema de numeración ordinal, no posicional y emplea letras mayúsculas como símbolos para representar los números; de esta manera, los números se escriben como combinaciones de letras. Así, por ejemplo, el año 2016 se escribe como MMXVI, en donde la ‘M’ representa 1000, la ‘X’ representa 10 más, la ‘V’ representa cinco unidades más y la ‘I‘ una unidad más.
La tabla inferior muestra los símbolos utilizados en el sistema de numeración romana, así como sus equivalencias en el sistema decimal:
|
ROMANO |
DECIMAL |
|
I |
1 |
|
V |
5 |
|
X |
10 |
|
L |
50 |
|
C |
100 |
|
D |
500 |
|
M |
1000 |
Los romanos desconocían el cero, número que fue introducido con posterioridad por los árabes, por lo que no existe ningún símbolo en el sistema de numeración romano que represente el valor cero.
Los numerales romanos se escriben, a día de hoy, con letras del alfabeto romano, pero en un principio eran símbolos independientes. Los etruscos, por ejemplo, usaron I, Λ, X, ⋔, 8 y ⊕ para representar I, V, X, L, C, y M, respectivamente, de los cuales sólo la I y la X eran letras de su alfabeto. Según algunos, la V representaba una mano y la X se formaba colocando una V del derecho encima de otra V invertida. No obstante, parece que los numerales etrusco-romanos vienen realmente de muescas o rayas que se tallaban en varas o palos para llevar los conteos (usados por los pastores, tanto dálmatas como italianos, hasta el siglo XIX).
De esta manera, el numeral 'I' no provendría de la letra 'I' sino de una muesca tallada en un palo o vara. Cada quinta muesca era una doble muesca (⋀, ⋁, ⋋, ⋌, etc.) y cada décima muesca era un tache (X), muy al estilo de las marcas de conteo europeas actuales. Esta sistemática originó un sistema posicional, como veremos a continuación.
Así, por ejemplo, ocho sobre una vara de cuentas eran ocho unidades (es decir ‘IIIIΛIII’), o la octava de una serie mayor de conteos, y se podía abreviar ‘ΛIII’ (o ‘VIII’), ya que la existencia de Λ implicaba cuatro muescas anteriores.
Para representar el dieciocho, dado que es la octava muesca después de las primeras diez, se puede abreviar con ‘X’, por lo que se escribe ‘XΛIII’ (o ‘XVIII’).
Igualmente, el número cuatro en una vara o palo, es la marca de ‘I’ que se coloca justo antes del corte de la ‘Λ’ (o ‘V’), así se puede escribir ‘IIII’ o ‘IΛ’ (o ‘IV’).
Cuando las cuentas se transfirieron a la escritura, las marcas se identificaron fácilmente con las letras romanas existentes ‘I’, ‘V’ y ‘X’.
La décima ‘V’ o ‘X’ sobre una vara o palo, recibía un trazo extra, así, el 50 se escribía de diferentes maneras: N, И, K, Ψ o ⋔, pero tal vez el más frecuente era una forma como una flecha apuntada hacia abajo, como una ‘V’ y una ‘I’ sobrescrita: ‘ᗐ’; durante la época del emperador Augusto, este grafismo se había achatado hasta formar una ⊥ (una T invertida) y, poco después, se identificó con la letra ‘L’, a la que se parecía gráficamente. De igual manera, el cien se escribía de distintas formas: Ж, ⋉, ⋈, H, pero llegó a predominar la forma ‘Ж’ (o sea una ‘X’ y una ‘I’ sobrescrita) y se escribía ‘>I<’ o bien ‘ƆIC’, luego se abrevió a ‘Ɔ’ o bien ‘C’, y la variante ‘C’ fue la que finalmente se impuso porque, como letra, representaba la abreviación de centum, que en latín significa “cien”.
Cuando se juntaban cien ‘V’ o cien ‘X’, la centésima ‘X’ o ‘V’ se marcaba con un recuadro o un círculo. Así, el 500 era como una ‘Ɔ’ sobrescrita con una ‘⋌’ o una ‘⊢’, es decir, como una ‘Þ’ con una línea recta horizontal por el medio, convirtiéndose en una ‘D’ (o una’ Ð’) durante la época del emperador Augusto, y devino en la letra ‘D’.
Por otro lado, el mil era una X encerrada en un círculo o un cuadrado: Ⓧ, ⊗, ⊕, y para la época agustina, se identificó con la letra griega ‘Φ’ (phi). Algunas variantes de este grafismo, fueron ‘Ψ’ y ‘CD’, y con el tiempo, la etimología popular identificó la ‘D’ con la mitad gráfica del símbolo Φ representativo del mil (debido a la variante CD). Un tercer grafismo de ‘CD’ sobrevivió, hasta hoy, en dos variantes:
- La primera ‘CIƆ’ llevó a la convención de usar paréntesis para indicar la multiplicación por mil: el original CIƆ = (I) 1000, luego (III) = 3000, (V) 5000, (IX) 9000, (X) 10 000, (L) 50 000, (C) 100 000, (D) 500 000, (M) 1000 000, etcétera; este sistema se extendió luego a paréntesis dobles, como ↁ, ↂ, etcétera.
- La otra variante del símbolo ‘CD’ se convirtió en ∞ y en ⋈, cambiando finalmente a una ‘M’, bajo la influencia de la palabra latina mille, que significa “mil”.
7. Los números en la cultura azteca (1325 - 1521).
El imperio azteca (o imperio Mexica) apareció en Méjico, fruto de la integración de los pueblos Texcoco, Tlacopan y México-Tenochtitlan (o la Triple Alianza).
Los aztecas desarrollaron un sistema de numeración propio y su base era vigesimal, por lo que las cantidades se agrupaban en veintenas (de 20 en 20); era un sistema muy intuitivo y para conformar las cantidades, se servían de puntos, rayas y dibujos; de esta manera, por ejemplo, el número uno (1) podía representarse con un punto o un dedo, el número cinco (5) con una mano, el número veinte (20) con una bandera, el número cuatrocientos (400) se representaba con una pluma y el número 8000 con una bolsa o costal.
Conocían y utilizaban el número cero (0).
En los dos dibujos inferiores puede observar los números utilizados por los aztecas.
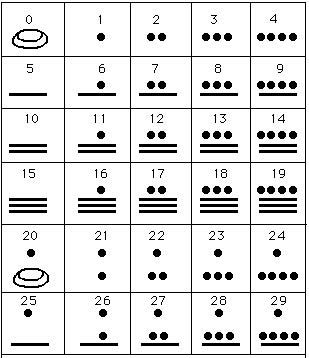

8. Los números de la cultura arábiga.
Los números arábigos, tal y como los conocemos ahora, son:
1, 2, 3, 4, 5, 6, 7, 8, 9 y el 0
Se trata de un sistema de tipo decimal cuyas cifras ocupan un lugar con un determinado valor, siendo el del símbolo cero el lugar destinado al vacío.
Todos conocemos la gran simplicidad que los números arábigos han traído al cálculo aritmético. La carga innecesaria de la que han liberado a la mente humana es incalculable. Frente a cualquier otro sistema de numeración inventado por el hombre, permiten una mayor facilidad de manejo debido a la presencia del cero.
Pero le llevó al hombre cerca de cinco mil años, a partir del comienzo de los símbolos numéricos, para concebir un símbolo que representase la nada. No se conoce quién fue su inventor, sin duda uno de los pensadores más creativos y originales de la historia. Sólo sabemos que fue un hindú que vivió antes del siglo IX d.C. Los hindúes denominaron a este símbolo “sunya”, que quiere decir nada o vacío y que fue adoptado por los árabes bajo la denominación de “sifr”, que en su idioma significaba lo mismo. Con el tiempo esta palabra se convertiría en “cefer”, más fácil de pronunciar. Finalmente dio origen en inglés a "cipher" y "zero" (esta última por intermedio de zefirum), así como a los vocablos castellanos cero y cifra.
A continuación pueden compararse los números hindi con los actuales. Como puede comprobarse, presentan ciertas similitudes.

Fue el matemático italiano Leonardo Fibonacci, quien durante la Edad Media aprendió este sistema de numeración adoptado y mejorado por los árabes. Hacia el año 1200, Leonardo Fibonacci vivía en Pisa, y para entonces los comerciantes de dicha ciudad mantenían lazos comerciales con las ciudades del Norte de África. Leonardo tuvo así la oportunidad de visitar aquellas regiones y conocer de manera directa este nuevo sistema de numeración. En 1202 publicó su tratado “Líber Abaci”, en el que se empleaba ese sistema y el símbolo “nada”, enseñando su uso en aritmética e introduciendo definitivamente estos números. Por aquel entonces en Europa se empezaba a salir de la oscura Edad Media, la prosperidad aumentaba y con ella el deseo de saber y de adquirir nuevos conocimientos. En Italia había numerosos comerciantes que necesitaban realizar continuos cálculos para mantener sus negocios y, en cuanto comprobaron las ventajas de los números “arábigos” (aunque su verdadera procedencia fuera hindú, se llamaron así porque los europeos los aprendieron del pueblo musulmán) adoptaron el nuevo sistema.
Debido a que estos números provenían de países que no usaban el alfabeto romano, sus grafismos eran muy diferentes a las de las letras latinas, y esto también resultó ventajoso, porque impidió que se confundieran con los números romanos, los cuales dejaron de utilizarse paulatinamente.
9. Los números en la cultura hebrea (200 a.C. – 250 a.C.).
En el sistema de numeración hebreo se utilizan las letras de su propio alfabeto; en este sistema de numeración, los valores numéricos de cada letra individual se suman de manera conjunta; de esta manera, a cada unidad (1, 2, 3, 4, 5, 6, 7, 8, 9) se le asigna una letra separada, y lo mismo ocurre con las decenas (10, 20, 30, 40, 50, 60, 70, 80, 90) y las centenas (100, 200, 300, 400, 500, 600, 700, 800, 900). En la práctica, la numerología hebraica (conocida como gematría) utiliza esta sistemática para el estudio de los textos sagrados judaicos, como son la Torá y el Talmud.
|
Letra hebrea |
Nombre de la letra |
Valor |
|
א |
||
|
ב |
||
|
ג |
||
|
ד |
||
|
ה |
||
|
ו |
||
|
ז |
||
|
ח |
||
|
ט |
||
|
י |
||
|
כ |
||
|
ל |
||
|
מ |
||
|
נ |
||
|
ס |
||
|
ע |
||
|
פ |
||
|
צ |
||
|
ק |
||
|
ר |
||
|
ש |
||
|
ת |
||
|
ך |
||
|
ם |
||
|
ן |
||
|
ף |
||
|
ץ |